Множество целых чисел — , определяется как замыкание множества натуральных чисел  относительно арифметических операций сложения (+) ивычитания (−). Таким образом, сумма, разность и произведение двух целых чисел дает снова целые числа. Оно состоит из натуральных чисел (1, 2, 3…), чисел вида 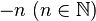 и числа ноль.

Необходимость рассмотрения целых чисел продиктована невозможностью (в общем случае) вычесть из одного натурального числа другое. Целые числа являются кольцом относительно операций сложения и умножения.

Отрицательные числа ввели в математический обиход Михаэль Штифель (1487—1567) в книге «Полная арифметика» (1544), и Николя Шюке (1445—1500).

Множество всех целых чисел обозначают знаком  от нем. Zahlen — числа.

 не замкнуто относительно деления двух целых чисел (например, 1/2). Следующая таблица иллюстрирует несколько основных свойств сложения и умножения для любых целых a, b и c.

На языке общей алгебры первые пять вышеперечисленных свойств сложения говорят о том, что  является абелевой группой относительно бинарной операции сложения, и, следовательно, такжециклической группой, так как каждый ненулевой элемент  может быть записан в виде конечной суммы 1 + 1 + … 1 или (−1) + (−1) + … + (−1). Фактически,  является единственной бесконечной циклической группой по сложению в силу того, что любая бесконечная циклическая группа изоморфна группе .

Алгебраические свойства

Первые четыре свойства умножения говорят о том, что  — коммутативный моноид по умножению. Однако стоит заметить, что не каждое целое имеет противоположное по умножению, например, нет такого x из , что 2x = 1, так как левая часть уравнения чётна, а правая нечётна. Из этого следует, что  не является группой по умножению, а также не является полем. Наименьшее поле, содержащее целые числа, — множество рациональных чисел ().

Совокупность всех свойств таблицы означает, что  является коммутативным кольцом с единицей относительно сложения и умножения.

Обычное деление не определено на множестве целых чисел, но определено так называемое деление с остатком: для любых целых a и b, , существует единственный набор целых чисел qи r, что a = bq + r и , где |b| — абсолютная величина (модуль) числа b. Здесь a — делимое, b — делитель, q — частное, r — остаток. На этой операции основан алгоритм Евклиданахождения наибольшего общего делителя двух целых чисел.